Assignment 14: Huffman Coding
A character encoding is a way of representing an alphabet (set of characters) with some kind of code. In computer science, that code is often made of single bits, 0s and 1s, since that is how all data is ultimately stored.
Unicode’s industry-standard encoding is what lets us have emojis. :-)
For example, if you had the following encoding:
Letter |
| Code |
a |
| 0 |
b |
| 1,0 |
c |
| 1,1 |
Then "abc" would be encoded as the five bits 01011, and 1110 would be decoded as "cb".
There are far fewer short codes than long codes. Why is this?
While there are various properties that make Huffman codings interesting, the one that is most helpful is that it is a prefix code. This means that no encoding of one character is a prefix of any other character’s encoding. The example given above is a prefix code. The following, however, is not:
Letter |
| Code |
e |
| 0 |
f |
| 1 |
g |
| 01 |
What would 01 decode to, ef or g? Prefix codes help eliminate these types of ambiguities.
14.1 The algorithm
The best way to explain the Huffman coding algorithm is to illustrate it.
For example, say you begin with the following letters:
"a", "b", "c", "d", "e", "f"
Where each letter has the following relative frequencies:
12, 45, 5, 13, 9, 16


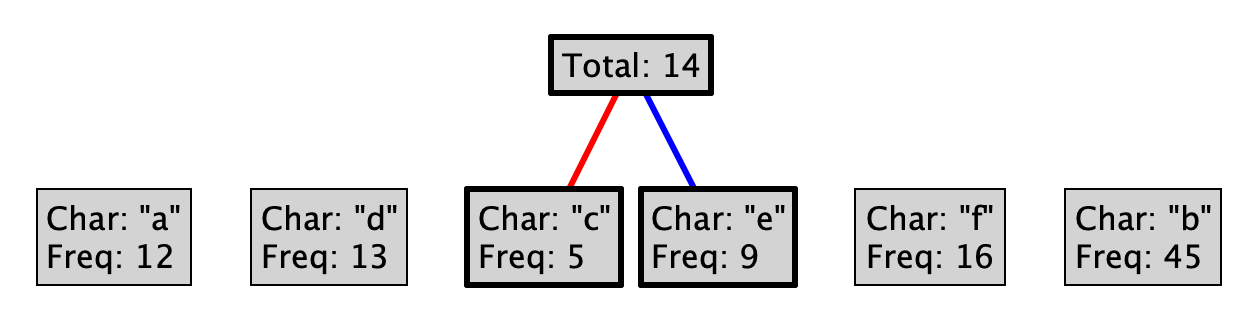
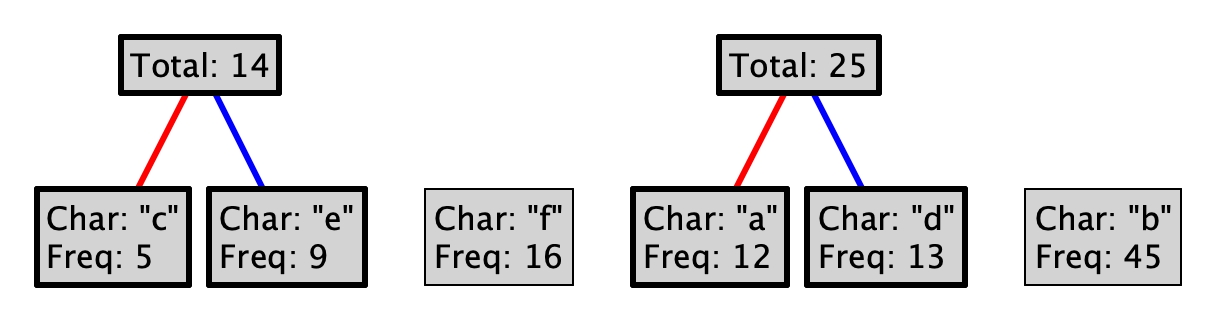
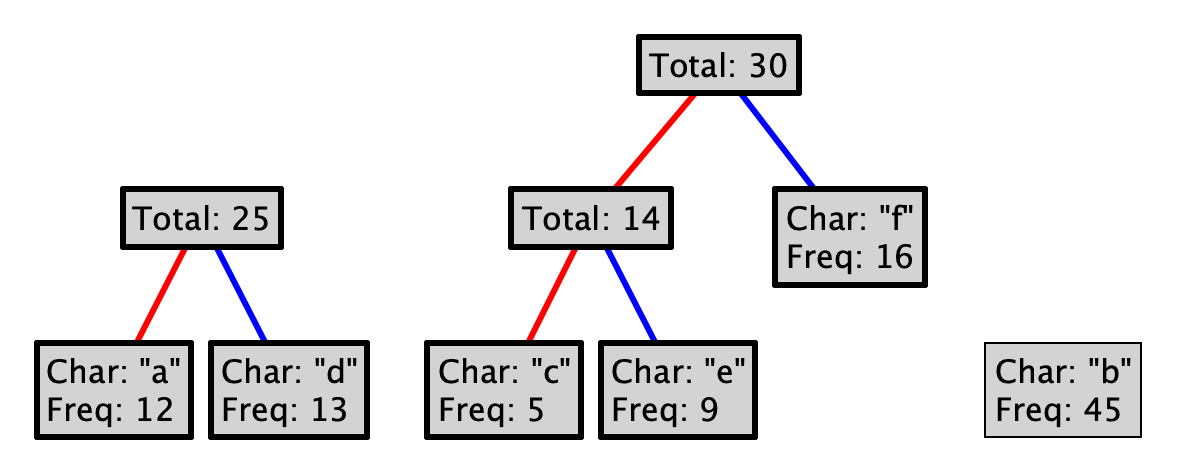
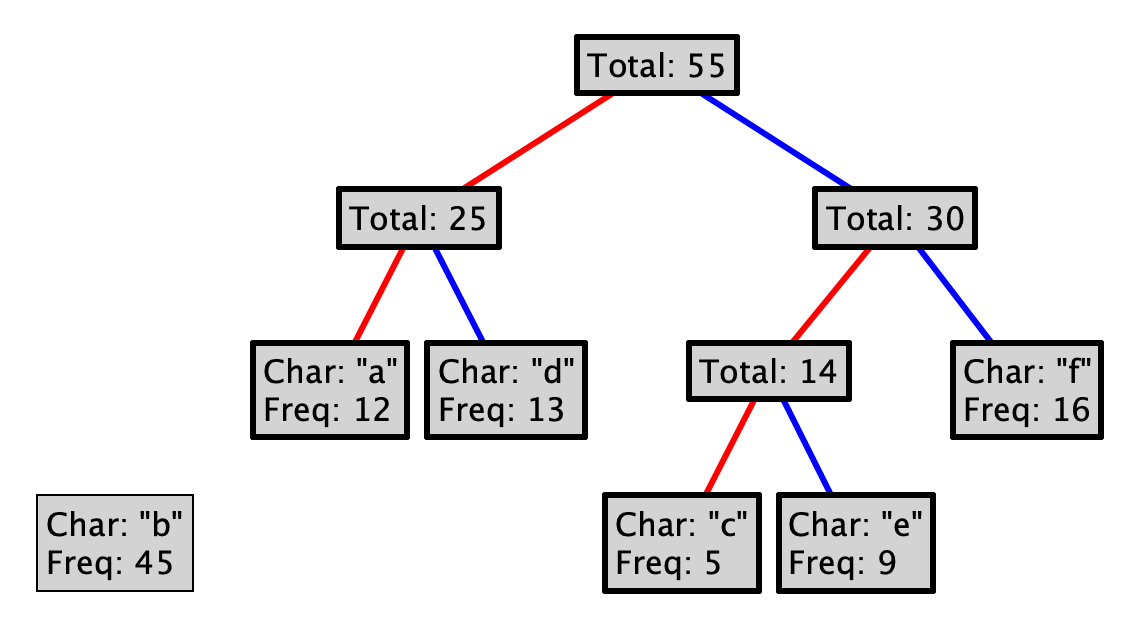
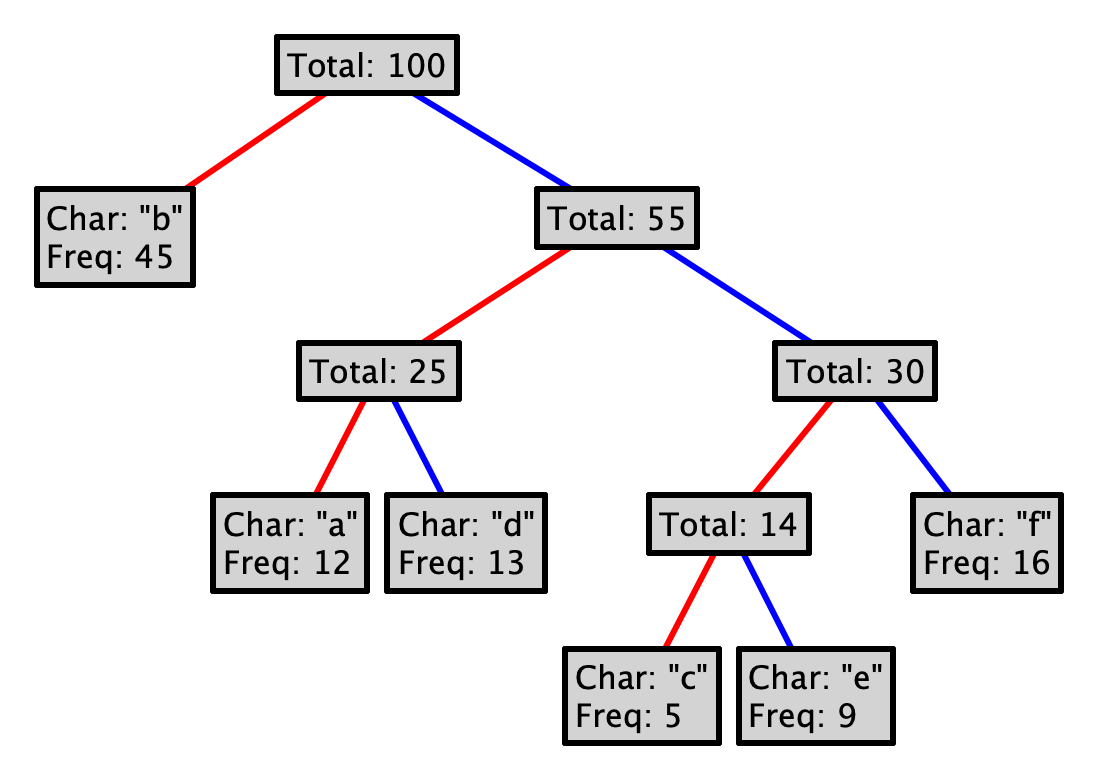
This process is guaranteed to produce a prefix code. Why? Could you choose red as 1, and blue as 0? Could you choose differently at every level of the tree?
To encode a character, follow the path from the root to the leaf with that letter, where a red line represents a 0, and a blue a 1. So, encoding "eba" with the tree above would produce 11010100. Decoding a sequence of 0s and 1s is (essentially) the inverse operation, so decoding 101111 would yield "df".
Composing the encoding and decoding operations in either order should produce what is effectively the identity function (on either strings or bit-sequences), but they aren’t quite inverse functions. Why not?
14.2 Data design
Design the Huffman class, which should be constructed with two ArrayLists, one of strings and the other of integers (in that order), representing the letters of the alphabet in question and their relative frequencies. You may assume the integers are always positive and that the strings are always of size 1 (and never equal to "?"), but you should throw an IllegalArgumentException if the lists are of different lengths or if the length of the list of strings is less than 2 (after all, there wouldn’t be much point of encoding a 1-letter alphabet).
Your forest should be represented by an ArrayList of some kind. You may need a helper class; you may need multiple ArrayLists; the design is up to you.
To achieve a consistent encoding, the leaves and nodes must be sorted consistently. When sorting the initial leaves, you should use a stable sorting algorithm. This means that if two different elements have the same value for the purposes of sorting, their relative order in the original list should be preserved. (For instance, if two letters have the same frequency, then they have the same value for sorting even though they are not the same letter.)
Similarly, when you insert a new node into the forest, you should ensure that it appears as deep in the list as possible, so that if it ties with something else already in the list, the existing value "wins" and should come first. You should be sure to carefully test these properties of your sort, and you should not have to attempt to re-sort the entire list when inserting a new node.
- Hint: To achieve this, design the following methods:
// sort a list of ITrees in ascending order by frequency void sort(ArrayList<ITree> trees) {} // insert tree into an array list of trees that are sorted along the range [0, maxIndexPossible) // 0 <= maxIndexPossible <= sortedTrees.size() // after this method, the list is sorted along the range [0, maxIndexPossible] void insert(ITree tree, ArrayList<ITree> sortedTrees, int maxIndexPossible) {} // insert the tree into this completely sorted list so that the final list is also completely sorted void insert(ITree tree, ArrayList<ITree> sortedTrees) {}
14.3 Methods
Design the encode method, which takes a string and returns an ArrayList<Boolean>, where 0 is represented by false and 1 by true. If the string contains any character not in the alphabet, an IllegalArgumentException should be thrown with the exact error "Tried to encode <the character in question> but that is not part of the language.", where "<the character in question>" is replaced with the first character in the string that is not in the alphabet.
Design the decode method, which takes an ArrayList<Boolean>, where 0 is represented by false and 1 by true, and returns the string represented by this encoding. If at the end of the list of booleans you run out of booleans before you can reach a terminal node in the tree, you should end the string with a single "?". For example, in the above tree, the list of false, true, false, would decode to "b?".